Depois de tantas vezes recomendado, finalmente tive a oportunidade de começar a ler o livro Mostly Harmless Econometrics. Decidi como apoio ao meu estudo buscar resumir os conceitos e eventualmente agregar exemplos contendo código. Evidentemente, aqui só estarão conceitos chave e exemplos mínimos para ilustrar. Considere que todos os termos são tradução livre e eu já não lembro ou nunca soube qual é a tradução mais usada para o Português de alguns deles. Antes de começar, faz sentido deixar o link do Mastering Econometrics, curso que o autor do livro tem elaborado.
Nesta primeira parte irei cobrir os capítulos 1 e 2, que estão na parte I do livro “Preliminares” (Preliminaires).
O autor propõe um guia prático e define como a caixa de ferramenta básica da econometria:
- Modelos de regressão para controlar por algumas variáveis que poderiam esconder a relação causal que se tem interesse
- Variáveis instrumentais para análise de experimentos reais ou naturais
- Estratégias que usam diferenças-em-diferenças para controlar por variáveis não observáveis e omitidas
A partir de agora vamos seguir com o conteúdo na organização do livro.
Índice
Questões sobre questões (Questions about questions)
Que tipos de questões seremos capazes de responder?
As questões que sempre devemos fazer ao começar um projeto de pesquisa são:
Qual é:
- a relação causal que quero descobrir?
- o experimento ideal
- a estratégia de identificação
- modo de inferência
A primeira é sobre a questão que gostaríamos de responder: qual o efeito de educação superior no salário de uma pessoa? qual o efeito no resultado de um exame nacional de estudar-se em uma escola particular?. A segunda pergunta é mais imaginativa: se não houvesse qualquer restrição orçamentária ou ética, qual seria o experimento ideal para medir o efeito desejado? Ou seja, imagina que poderia-se alocar-se aleatoriamente pessoas para fazer ou não um curso superior, após alguns anos de formado, poderíamos saber a diferença média dos salários.
Identificação é como chamamos a atividade de identificar esse efeito que se deseja através de dados observacionais. A quarta pergunta é sobre modo de inferência - não ficou muito claro para mim as implicações dessa parte, mas será coberto em algum momento.
O ideal experimental (The experimental ideal)
O intuito desta secção é mostrar o experimento aleatório como padrão de comparação e dar intuições do porquê. Para entender a importância, começamos com o conceito de viés de seleção (selection bias).
O problema da seleção (The selection problem)
Para ilustrar os próximos conceitos, é utilizado um exemplo em que se quer saber o efeito de ir ao hospital para a saúde de pessoas idosas.
De um lado, imagina-se que ir ao hospital significa receber cuidados e que isso contribuirá para a saúde. Do outro, também tem-se o fato de que é um ambiente periogoso para uma população de risco, como idosos. A informação dada pela NHIS (National Health Interview Survey) possui os seguintes resultados:
| Groupo | Tamanho amostral | Estado médio de saúde | Desvio padrão |
|---|---|---|---|
| Hospital | 7774 | 2.79 | 0.014 |
| Sem Hospital | 90049 | 2.07 | 0.003 |
Percebe-se que a diferença entra a média do estado de saúde é 0.72 e que ela é melhor para aqueles que não vão para o hospital. Não se pode concluir tão rápido que não ir ao hospital é a coisa certa a se fazer. É preciso atentar que grupo que vai e que não vai são antes da decisão do tratamento diferentes e que não são distribuidos entre as duas opções aleatoriamente. Apenas pessoas com pior estado de saúde vão para o hospital. Lembrando que “tratamento” é o termo geral que usamos para a ação que estamos estudando, embora aqui a ação seja ligada com tratamento de saúde.
Para este estudo, definiremos como Resultado o estado de saúde da pessoa, colocarei como apenas saúde. O tratamento será \(D\). Temos:
\[\text{Resultado Potencial} = \begin{cases} Y_{1i} \mbox{, se } D_{i} = 1 \\ Y_{0i} \mbox{, se } D_{i} = 0 \\ \end{cases}\]O Resultado Potencial é sobre o que teria sido observado para uma pessoa se ela tivesse recebido o tratamento (\(Y_{1i}\)), sem se importar se ela na realidade recebeu ou não. A idéia de potencial é que ela seria a quantidade observada caso o tratamento fosse ou não aplicado. Já o resultado é apenas sobre o que foi observado, o que aconteceu de fato:
\[\text{Resultado}, Y_{i} = \begin{cases} Y_{1i} \mbox{, se } D_{i} = 1 \\ Y_{0i} \mbox{, se } D_{i} = 0 \\ \end{cases}\]\begin{equation} = Y_{0i} + (Y_{1i} - Y_{0i})D_{i} \end{equation}
É interessante notar que o que adoraríamos responder, que é o efeito de ser hospitalizado para um determinado indivíduo \(i\), é a quantidade \(Y_{1i} - Y_{0i}\), que é a diferença entre os resultados potenciais de ser ou não tratado. Porém, nunca poderemos observar o resultado \(Y_{i}\) sob as duas possibilidades para \(D_{i}\). Portanto, é necessário usar de alguma forma as pessoas que foram e não tratadas para estimar um efeito médio.
A quantidade que calculamos 0.72 entre as médias é útil quando feita usando as definições acima para entendermos o que está acontecendo:
\[\begin{align} \begin{split} \mathbb{E}[Y_{i} \mid D_{i}=1] - \mathbb{E}[Y_{i} \mid D_{i} =0] ={}& \mathbb{E}[Y_{0i} + (Y_{1i} - Y_{0i}) \mid D_{i} = 1] - \mathbb{E}[Y_{0i} \mid D_{i} = 0] \\ ={}& \mathbb{E}[Y_{0i} \mid D_{i} = 1] + \mathbb{E}[(Y_{1i} - Y_{0i}) | D_{i} = 1] - \mathbb{E}[Y_{0i} \mid D_{i} = 0] \\ ={}& \mathbb{E}[Y_{0i} \mid D_{i} = 1] + \mathbb{E}[Y_{1i} | D_{i} = 1] - \mathbb{E}[Y_{0i} | D_{i} = 1] - \mathbb{E}[Y_{0i} \mid D_{i} = 0] \\ ={}& \mathbb{E}[Y_{1i} | D_{i} = 1] - \mathbb{E}[Y_{0i} | D_{i} = 1] \ \text{(Efeito médio do tratamento nos tratados)}\\ {}& + \mathbb{E}[Y_{0i} \mid D_{i} = 1] - \mathbb{E}[Y_{0i} \mid D_{i} = 0] \ \text{(Viés de seleção)} \end{split} \end{align}\]O primeiro termo, efeito médio do tratamento nos tratados, nos diz qual é o efeito de receber tratamento para uma pessoa que buscaria ser hospitalizada. Ou seja, dado que ela iria para o hospital, qual é a diferença entre o resultado potencial de ir e não ir.
Já o segundo termo, o viés de seleção, é a diferença do estado de saúde médio de pessoas que vão ou não para o hospital. Como pessoas mais doentes são as que costumam ir, é esperado que essa subtração de um resultado negativo, pois \(\mathbb{E}[Y_{0i} \mid D_{i} = 1] < \mathbb{E}[Y_{0i} \mid D_{i} = 0]\), ou seja, o efeito do tratamento seria subtraído pelo viés. Sendo assim, há a possibilidade do viés ser tão grande que o efeito médio do tratamento seria subtraído por um valor maior e o efeito final que teríamos seria negativo. E é assim que o viés de seleção impossibilita essa abordagem.
Experimentos aleatórios resolvem o problema (Random Assignment Solves the Selection Problem)
Um experimento aleatório é quando decidimos as pessoas que serão tratadas ou não de forma aleatória, sem usar qualquer informação. Ou seja, a pessoa seria hospitalizada independentemente do seu estado de saúde - esse exemplo absurdo já mostra um pouco do porquê nem sempre podemos fazer isso.
Ao usar um experimento aleatório nós tornamos \(Y_{i}\) independente de \(D_{i}\), o que nos permite trocar \(\mathbb{E}[Y_{0i} \mid D_{i} = 1]\) por \(\mathbb{E}[Y_{0i} \mid D_{i} = 0]\), por exemplo. Dessa forma, temos que:
\[\begin{align} \begin{split} \mathbb{E}[Y_{i} \mid D_{i}=1] - \mathbb{E}[Y_{i} \mid D_{i} =0] ={}& \mathbb{E}[Y_{1i} | D_{i} = 1] - \mathbb{E}[Y_{0i} | D_{i} = 1] \ \text{(Efeito médio do tratamento nos tratados)}\\ {}& + \mathbb{E}[Y_{0i} \mid D_{i} = 1] - \mathbb{E}[Y_{0i} \mid D_{i} = 0] \ \text{(Viés de seleção)} \\ ={}& \mathbb{E}[Y_{1i} | D_{i} = 1] - \mathbb{E}[Y_{0i} | D_{i} = 1] \\ {}& + \mathbb{E}[Y_{0i} \mid D_{i} = 1] - \mathbb{E}[Y_{0i} \mid D_{i} = 1] \\ ={}& \mathbb{E}[Y_{1i} | D_{i} = 1] - \mathbb{E}[Y_{0i} | D_{i} = 1] \\ {}& + 0 \\ ={}& \mathbb{E}[Y_{1i}] - \mathbb{E}[Y_{0i}] \\ ={}& \mathbb{E}[Y_{1i} - Y_{0i}] \\ \end{split} \end{align}\]Isso mostra que o viés de seleção é eliminado quando existe independência de \(D_{i}\) do resultado potencial. É um grande passo para que se possa calcular efeitos causais, embora experimentos aleatórios não sejam sempre possíveis e mesmo quando o são possuem seus próprios desafios.
Análise de regressão para experimentos (Regression Analysis of experiments)
Vamos ver agora como uma regressão traduz o efeito de um tratamento.
\[\begin{align} & Y_{i} = \alpha + \rho D_{i} + \eta_{i} \\ \\ \text{Onde: } \\ & Y_{i}: Resultado \\ & \alpha: \mathbb{E}[Y_{0i}] \\ & \rho: Y_{1i} - Y_{0i} \\ & \eta_{i}: Y_{0} - \mathbb{E}[Y_{0}] \ \text{(A parte aleatória de } Y_{0i} \text{)}\\ \end{align}\]Fazendo a \(\mathbb{E}\) condicionada em \(D_{i} = 1\) e em \(D_{i} = 1\) (em dois processos separados!), temos:
\[\mathbb{E}[Y_{i} \mid D_{i} = 1] = \alpha + \rho + \mathbb{E}[\eta_{i} \mid D_{i} = 1] \\ \\ \mathbb{E}[Y_{i} \mid D_{i} = 0] = \alpha + \mathbb{E}[\eta_{i} \mid D_{i} = 0] \\\]Ao subtrairmos um do outro, teríamos:
\[\begin{align} \begin{split} \mathbb{E}[Y_{i} \mid D_{i} = 1] - \mathbb{E}[Y_{i} \mid D_{i} = 0] = & \ \rho \ \ \text{(Efeito causal)} \\ &+ \mathbb{E}[\eta_{i} \mid D_{i} = 1] - \mathbb{E}[\eta_{i} \mid D_{i} = 0] \ \ \text{(Viés de seleção)} \\ \end{split} \end{align}\]O viés de seleção é a correlação entre o termo de erro da regressão, \(\eta\), e o regressor \(D\), que representa o tratamento. Ele reflete a diferença que há entre a média de \(Y_{0i}\) para quem é tratado e para quem não é tratado. De forma que:
\[\mathbb{E}[\eta_{i} \mid D_{i} = 1] - \mathbb{E}[\eta_{i} \mid D_{i} = 0] = \mathbb{E}[Y_{0i} \mid D_{i} = 1] - \mathbb{E}[Y_{0i} \mid D_{i} = 0] \\\]Desta forma, novamente, quando temos um experimento aleatório este termo é excluído e ficamos apenas com o efeito do tratamento expresso em \(\rho\). Assim, podemos estimar uma regressão neste formato e usar o parâmetro estimado para \(D\) como o efeito médio do tratamento.
O capítulo possui um exemplo com dados de Krueger (1999), que podem ser encontrados aqui. Este é o paper de base. Como estava ansioso pra rodar algo do livro, tentei reproduzir o que foi feito, porém, os dados não estão exatamente da forma que o autor tinha ao dispor, sendo que uma delas é crítica para a reprodução, que é a escola a qual pertence o aluno:
The independence between class-size assignment and other variables is only valid within schools, because randomization was done within schools. Consequently, a separate dummy variable is included for each school to absorb the school effects, a alpha i.
Aqui o autor diz que a independência entre a determinação da sala e as outras variáveis só é válida dentro de cada escola, pois a aleatoriazação foi feita escola por escola, ou seja, características da escola podem ser usadas para prever se o aluno foi alocado para uma sala menor, com monitoria ou normal, pois a probabilidade de cada uma dado as características das escolas é diferente.
Imagine que você pega um aluno aleatório do experimento, como as escolas possuem características que tornam diferentes as condições iniciais do estudo pela quantidade e distribuição dos alunos, a forma como eles são alocados em cada turma do experimento é diferente entre elas, e saber a escola de onde esse aluno veio faz com que a chance dele ter sido marcado para ir para um tipo de classe diferente seja mais ou menos provável, enquanto a informação da escola não deveria ser capaz de nos ajudar em nada nessa tarefa.
Para conseguir controlar pelo efeito que vem de características de cada escola, foi criada uma vairável para representar qual era a escola daquele exemplo. Ou seja, todo o efeito que possa existir dessa diferença vai ficar representado no \(\beta\) que acompanhará esta variável.
É interessante ainda passar pelo o que é apresentado no paper para reforçar como o experimento aleatório nos ajuda: ao tornar a variável de alocação no tamanho da sala aleatória, ela se torna não correlacionada com as variáveis presentes, mas também com as variáveis omitidas, o que faz com que não tenhamos problemas com o viés causado por variáveis omitidas em seu parâmetro \(\beta\).
Pesquisadores que buscaram reproduzir o estudo tentaram fazer uma inferência sobre quais alunos eram da mesma escola.
No meu caso, só fiz a transformação do target (média das notas) de acordo com a descrição no artigo (embora uma das três notas não esteja no dataset), rodei a regressão com as variáveis binárias para a presença em uma sala reduzida ou em uma sala com monitoria.
De qualquer forma, aqui temos um exemplo de como realizar uma regressão utilizando os dados:
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from statsmodels.regression.linear_model import OLS
from sklearn.preprocessing import OneHotEncoder, quantile_transform, MinMaxScaler
from statsmodels.tools import add_constant
from scipy import stats
# Lendo os dados
data = pd.read_stata("webstar.dta")
# Normalizando a nota das provas
class_types = ["small class", "regular + aide class", "regular class"]
test_types = ["tmathss", "treadss"]
grade = "k"
regular_data = data[data["cltype" + grade].isin(class_types[1:])]
small_data = data[data["cltype" + grade].isin([class_types[0]])]
for test_type in test_types:
new_column = "regularized_" + test_type + grade
original_column = test_type + grade
regular_data.loc[:, new_column] = regular_data[original_column].apply(lambda x: scoreperc(regular_data[original_column], x))
small_data.loc[:, new_column] = small_data[original_column].apply(lambda x: scoreperc(regular_data[original_column], x))
regularized_data = pd.concat([small_data, regular_data])
data = data.merge(regularized_data[[new_column]], right_index=True, left_index=True, how="left")
data["sat_score"] = data[["regularized_" + test_type + "k" for test_type in test_types]].mean(axis=1)
data = data[~pd.isnull(data["sat_score"])]
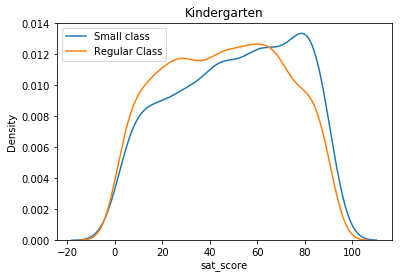
Não tenho certeza se consegui traduzir exatamente a transformação que o autor diz ter feito no target, aqui está a comparação para o Kindergarden:
data["small_class"] = (data["cltypek"] == "small class").astype(int)
data["aide"] = (data["cltypek"] == "regular + aide class").astype(int)
### Função auxiliar para realizar a regressão
def regression(data, regressors, dependent):
X = add_constant(data[regressors])
model = OLS(data[dependent], X, missing="drop", hasconst=True)
results = model.fit()
return results
### Parâmetros que usaremos na função
regressors = ["small_class", "aide"]
dependent = "sat_score"
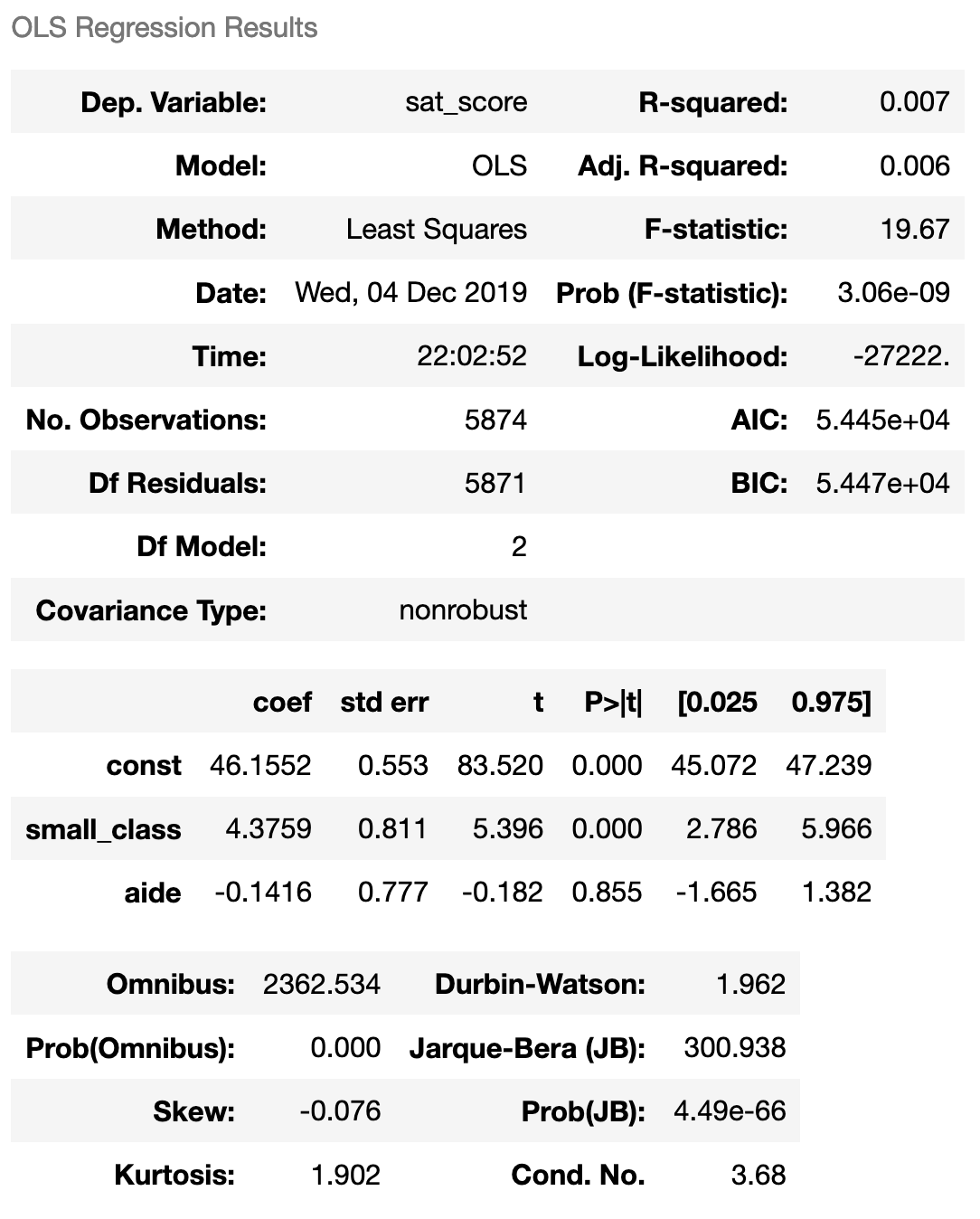
result = regression(data, regressors, dependent)
result.summary()
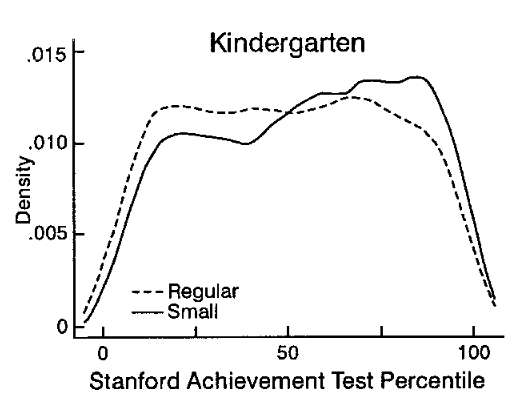
Os resultados do paper foram:
Ou seja, esperaríamos um intercepto de 4.82, porém, o resultado ficou um pouco diferente deste e o valor para a monitoria também ficou fora. Lembrando, uma das notas não estava presente no dataset, como a diferença não foi tanta, é possível que seja esta a única diferença.
E por esse capítulo é só!