Neste texto pretendo abordar o significado de bias para ciência de dados. Para tal, irei passar pelo mesmo conceito nas áreas que compõe e se relacionam com o objetivo.

1. Significado de bias
2. Bias em estatística
3. Aprendizado de Máquina
4. Ciência de dados 4.1 Com quem a máquina está aprendendo? 4.2 Estudos de caso
5. Ética e justiça
6. Bibliografia

Significado de Bias

A tradução de bias para o português é viés, cujo significado é:

Vi-és (francês biais)

1. Linha, trajectória ou direcção oblíqua. = OBLIQUIDADE
2. Tira estreita de tecido cortada obliquamente da peça.
3. Tendência ou carácter de algo.
4. Distorção ou tortuosidade na maneira de observar, de julgar ou de agir.

Os significados mais relevantes para um contexto de dados são o de tendência e distorção.

Bias em estatística

A primeira vez que a maioria dos cientistas de dados ouviu o termo “bias” foi provavelmente em aulas introdutórias de estatística. Qual o significado de bias em um livro de estatística básica? É o de desvio sistemático do valor real. É desvio por não coincidir com o valor real e é sistemático por acontecer consistentemente, em média.

Então é dito que um estimador, ou seja, uma abordagem para estimar (encontrar uma aproximação de algo) de um parâmetro, que é uma característica real de algo, como a média de uma população, é não viesado se na média o estimador é igual ao valor real. Seja \(\hat{\theta}\) um estimador e \(\theta\) o parâmetro a ser estimado:

\[\begin{equation} \mathbb{E}[\hat{\theta}] = \theta \end{equation}\]

Essa característica poderia ser a média dos estudantes brasileiros em um exame nacional. A população são os estudantes brasileiros e você quer estimar a média nacional perguntando apenas para parte deles. A média amostral é um estimador não viesado. O que isso quer dizer? Que se tirarmos amostras aleatórias dos estudantes e perguntarmos suas notas, a média desses valores irá “flutuar” em torno na média real e irá convergir para esta com o aumento do número de estudantes nessa amostra.

Até aqui estamos falando do viés que pode estar ou não contido no estimador, isto é, na abordagem que estamos usando para acessar o valor real de um parâmetro que é desconhecido para nós - que é impossível ou muito custoso de ser medido diretamente.

Da mesma forma, quando queremos decompôr um fenômeno em uma relação linear com uma regressão linear, quer-se estimar como cada variável independente contribui na formação da variável dependente. Então há uma noção de que existe uma relação verdadeira expressa como:

\[\begin{equation} y = \beta_{0} + \beta_{1} * x_{1} + \beta_{2} * x_{2} + ... \end{equation}\]

Mas como não temos acesso direto à essa equação, nós gostaríamos de estimá-la, sendo assim, buscamos algo como:

\[\begin{equation} y = \hat{\beta_{0}} + \hat{\beta_{1}} * x_{1} + \hat{\beta_{2}} * x_{2} + ... + \epsilon \end{equation}\]

Novamente, quer-se um estimador que não seja viesado, que seu valor esperado seja igual ao real. Além disso, é preferível, entre todos os não viesados, que a variância seja a menor possível. Graficamente ¹:

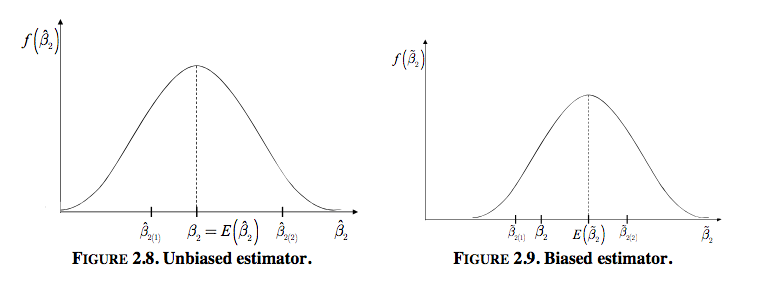
Segundo o Gauss-Markov theorem ², se os erros \(\epsilon\) do modelo de regressão linear:

• Possuem média zero: \(\mathbb{E}[\epsilon] = 0\)
• São Homocedásticos, ou seja, todos possuem a mesma variância e ela é finita: \(Var(\epsilon_{i}) = \sigma^{2} < \inf\)
• Termos distintos são não correlacionados: \(Cov(\epsilon_{e}, \epsilon_{j}) = 0, \forall i \neq j\)

Ao estimarmos esses parâmetros usando ordinary least squares (OLS), teremos o melhor estimador linear não viesado (best linear unbiased estimator - BLUE).

Portanto, até aqui estamos chamando de não viesada as técnicas que utilizamos para estimar dizemos que isso é uma propriedade delas.

Muito provavelmente

Aprendizado de Máquina

Um dos grandes temas em aprendizado de máquina é o trade-off entre viés e variância (Bias x Variance), que reflete também no sub-ajuste e sobre-ajuste (underfitting e overfitting).

O erro de generalização de um algoritmo de aprendizado, o quão bem ele pode prever novos casos, pode ser decomposto em viés e variância.

O viés também é chamado de erro sistemático, pois ele é sobre o algoritmo não ser capaz de expressar a forma funcional com que aquele fenômeno se dá. Ou seja, por mais que usemos amostras diferentes ou maiores, ele nunca se aproximará do valor real que queremos estimar, pois não é capaz.

Já a variância é chamada também de erro aleatório, pois captura nuânces das amostras, uma vez que tende a construir regras complexas demais sem a quantidade de exemplos necessária para tal.

Portanto, para um mesmo exemplo, se temos um modelo com o viés alto (underfitting), o erro será alto, mas causado por regras simples. Se for feito amostragens aleatórias do conjunto de treinamento (bootstraping) e treinarmos 10 modelos, teremos 10 previsões muito parecidas entre si, porém, todas serão ruins.

Já no caso de um modelo com o erro de variância alto, ou seja, no caso do overfitting, se fizermos o _bootstrap__ teremos 10 previsões bem diferentes entre si, porém, algumas podem passar bem próxima do valor real, enquanto outras passariam longe. De forma que não teríamos a garantia se estamos em um caso bom ou ruim, tendo que conviver com a aleatoriedade dessa estimação.

É preciso aumentar a complexidade do modelo de acordo com a disponibilidade de dados para construir regras complexas o suficientes para explicar o fenômeno, que possuam poder de generalização. E é assim que nós aceitamos viés nos modelos, pois em determinada medida é vantajoso Neste contexto o bias é sobre a previsão, sobre o quanto podemos estar distantes do valor real na média.

Portanto, nós aceitamos viés em modelos de aprendizado de máquina que tem como objetivo a previsão para que possamos minimizar o erro de generalização.

Aprendizado supervisionado

Antes de falar sobre viés nos dados é preciso falar um pouco sobre teoria do aprendizado supervisionado.

Basicamente, aprendizado supervisionado se resume na conexão de uma distribuição conjunta de variáveis \(X\) (as suas características, features, as colunas da sua tabela de dados) em uma variável alvo \(y\) (o target, uma determinada coluna da sua tabela e que você tem o interesse de prever). É suposto que haja um conjunto anotado de exemplos, ou seja, registros na sua tabela que possuam o valor de \(y\) para que possamos treinar um modelo que aprenderá a fazer essa conexão:

\[\begin{equation} X \rightarrow y \end{equation}\]

Qual o resultado obtido? Um modelo que é capaz de conectar novos exemplos vindos da distribuição conjunta \(X\) à valores de \(y\), ou seja, prevê-los, pois espera-se que você entregue um exemplo vindo de \(X\) antes de poder observar o valor real de \(y\), com o desempenho médio encontrado na etapa de validação enquanto construíamos o modelo.

Qualquer aplicação que esteja fora disso terá um comportamento diferente. E é sobre isso que falaremos nas próximas secções.

Ciência de dados

Vamos tratar essa secção como se fosse “aplicação de aprendizado de máquina”. Boa parte do que é chamado de ciência de dados hoje é sobre previsão. E previsões são feitas de modelos e dados.

Vamos considerar que o bias em relação à modelo é o relacionado ao trade off anteriormente explicado e que é uma questão teórica.

Portanto, de onde vem o que comumente temos ouvido como “efeitos preocupantes causados pelo bias em machine learning”?

Com quem a máquina está aprendendo?

Como dito, em aprendizado de máquina queremos aprender uma relação, um fenômeno: churn, inadimplência, ocorrência de uma doença e etc. E em aprendizado supervisionado precisamos de uma base anotada para dizer para máquina: “Tá vendo como as coisas acontecem? É assim! Agora eu quero que você aprenda todas as regras que dizem como as características podem prever cada caso.”. Mas como essa base foi anotada?

Digamos que queiramos construir um modelo para diagnosticar virose baseada nos sintômas dos pacientes. Agora precisamos de uma base que contenha uma série de sintômas e características de um paciente e uma anotação que diga “virose ou não”.

Para a nossa sorte, encontramos um médico muito cuidadoso que ao longo dos anos tomou nota de todas as suas consultas e fez questão de registrar as características dos pacientes e seus sintomas. Em uma série de casos, o seu diagnóstico foi de que o paciente estava com virose, em outros de que ele não possuia.

Pegamos essa base e alimentamos o modelo com as características (\(X\)) e dizemos que quando observamos aquilo o caso era de virose ou não (\(y\)). Treinado o modelo, o que teremos?

Uma máquina capaz de dizer se um novo paciente tem virose ou não? Não!

Teremos uma máquina capaz de imitar a maneira como o o médico do qual usamos a base de dados diagnostica virose! Com tudo que há de certo e errado nisso. Portanto, se esse médico em específico tem uma tendência a achar que é um caso de virose sempre o paciente apresenta náusea em uma frequência maior do que outros medicos o fariam, o nosso modelo levará esse viés consigo.

Mas que abordagem ruim! Não é melhor a gente ir direto nos casos que eram de fato virose?

Sim, este é o certo. Porém, nem sempre há o que possa ser considerado como verdade (ground truth) para um fenômeno. E, pior, há casos em que só se pode observar a variável alvo se uma decisão, que pode ter sido tomada baseada em um modelo, permitir, como é o caso de só poder observar a inadimplência em pessoas que recebem crédito. Ainda: pode ser que haja viés nos casos em que é possível observar o target: se você faz uma pesquisa para saber a renda das pessoas, as que se dispõe responder não são uma amostra aleatória, mas terão um viés.

E mesmo se o médico fizesse um esforço para melhorar as suas anotações e bolasse um esquema:

1. Se o paciente não voltar, o tratamento para virose funcionou e realmente era virose;
2. Se o paciente voltar, não era virose.

Porém, quem garante que a doença não curou-se de forma não relacionada com o tratamento? Ou que o paiente não voltou por ter ido em outro médico e buscar tratamento alternativo? Ou que ele voltou e o tratamento nào foi adequado ou aplicado da forma correta?

Temos, assim, que a variável alvo de um modelo de aprendizado supervisionado é principal fonte do que é chamado de viés em aprendizado de máquina, que consiste em um erro sistemático na previsão.

Das causas, podemos citar:

1. O fato de que um modelo necessariamente aprende com o passado e aplica as regras no presente, o que influencia o futuro e os novos dados que realimentarão os modelos. Portanto, ele propaga viéses do passado;
2. Regras, preconceitos e viéses são aprendidos pelos modelos se a variável alvo for “formada” usando anotações geradas pela ação de humanos;
3. Nem sempre é possível observar a formação da variável alvo e o modelo pode ser a causa disso. Um modelo que é usado para conceder crédito não vai possibilitar que se observe como bom pagado ou não uma pessoa que teve o crédito negado. Porém, continuamos aplicando para todos os pedidos de crédito atuais um modelo que foi treinado apenas com pessoas que receberam crédito no passado, estamos treinando e aplicando em distribuições \(X\) diferentes! Enfim, viés de seleção em geral: treinando em amostras não aletórias e aplicando em sub grupos ou populações diferentes.

Ainda aqui a preocupação é dividida entre uma questão prática que vai contra a teoria, com a diferença entre populações de treinamento e aplicação, e a sociedade em geral, que preocupa-se com qual é este viés que está sendo reproduzido pelo modelo e como ele afeta a vida das pessoas.

Estudos de caso

COMPAS

Em um dos casos mais famosos sobre viés em aprendizado de máquina temos o Correctional Offender Management Profiling for Alternative Sanctions (COMPAS), que era composto por um modelo para prever a probabilidade de reincidência criminal para indivíduos em julgamento.

A utilidade do modelo é que há um custo em manter em custódia alguém que não gerará dados à sociedade até que ele seja julgado, assim como é danoso deixar em liberdade quem irá comenter delitos neste tempo.

Porém, ao ter a sua efetividade analisada [^fn4], o modelo mostrou-se problemático de um ponto de vista racial. Em relação à acurácia, temos que o modelo apresentava uma acurácia de 67% para pessoas brancas, enquanto para pessoas negras era 63.8%. Isso pode parecer não muito preocupante à primeira vista, mas o cenário piora se abrimos essa métrica, pois os erros cometidos afetavam pessoas brancas e negras de formas diferentes.

O modelo previa erroneamente que uma pessoa negra sera reincidente em uma taxa de 44.9%, duas vezes maior do que a taxa para brancos (23.5%). E pessoas brancas que de fato tornavam-se reincidentes eram previstas como seguras em 47.7% dos casos, enquanto isso acontecia em apenas 28% dos casos para negros.

O que fica claro neste caso é que o viés não é sobre usar características para prever melhor, mas é sobre superestimar ou subestimar probabilidades utilizando viéses presentes na sociedade.

Amazon

A Amazon desenvolveu uma ferramental experimental para avaliar currículos automaticamente que envolvia aprendizado de máquina. O que foi percebido após um tempo é que mesmo não tendo o gênero explícito no modelo, ele aprendeu que palavras associadas teriam um impacto negativo, como fazer parte do clube de xadrez para mulheres, ou ter estudado em escolas apenas para meninas.

Diferente do caso da COMPAS, o que foi exposto neste caso foi uma característica que tinha impacto negativo e não qual seria o resultado do uso.

Houve a tentativa de deixar o algoritmo neutro, mas então ele aprendeu a ponderar positivamente palavras que era mais usadas por engenheiros homens do que mulheres, tais como “executed” e “captured”.

No final, este não era o único problema do modelo e ele acabou sendo descontinuado.

Que problemas causaram os viéses?

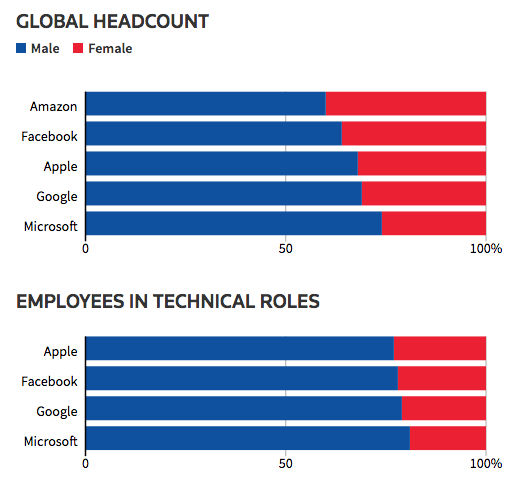
No mesmo artigo há um gráfico com a proporção de empregados homens em áreas técnicas em grandes empresas.

Na Google 79% dos funcionários em cargos técnicos são homens. Sendo assim, caso treinemos um modelo usando como label positiva os funcionários que foram contratados e tiveram um bom desempenho e como negativo os que não foram contratados e os que não performaram bem, é esperado que tendo uma maioria sendo homens, seria útil para o modelo saber distinguir se um candidato é homem ou mulher.

Imagine que você mesmo tivesse que realizar a tarefa de adivinhar entre um conjunto de currículos quais são funcionários de uma determinada empresa: ao saber que a maioria dos funcionários em uma empresa são homens, ter essa informação seria útil para ter uma boa performance nessa tarefa.

E isso parece péssimo e provavelmente é. O modelo quer maximizar os acertos e focar nos casos que representam a maioria parece uma boa estratégia.

O que é preocupante não é só que a diferença nas proporções contribuem para o tratamento desigual, mas também o viés que foi usado no passado para aprovar os funcionários está inserido no modelo. Embora não haja informações de como foram geradas as anotações, pode-se imaginar que algo assim pode ter acontecido.

Ética e justiça

Justiça em aprendizado de máquina e ciência de dados continua como um tema aberto. Embora a discussão sobre privacidade e uso de dados seja antiga, são novas as maneiras como dados tem sido usados e as suas consequências.

Por um lado, há a abordagem como um tema técnico: eliminar o bias estatístico dos modelos. Do outro, há a busca pela inserção de critérios no algoritmo que refletissem valores humanos.

Como visto no caso da Amazon, deixar o modelo cego para as características que não queremos que tenham influência não é suficiente.

O que seria uma previsão justa? Não é tão difícil levantar uma definição. O problema, na verdade. é levantar apeans uma definição que seja aceita e que possa guiar as ferrametnas atualmente utilizadas para ajustarem-se. Para ter uma idéia de como podem ser os diferentes critérios, veja essa apresentação com 21 deles!. Além disso, neste paper é possível ver as definições matemáticas.

Como exemplos, poderíamos citar ³:

Seja \(Y\) a anotação (label), \(S\) a probabilidade de pertencer a classe positiva, \(d\) a classe prevista, \(G\) o grupo sensível, vamos usar gênero, que é o exemplo do trabalho citado, mas poderia ser raça, religião e etc.

Paridade preditiva (predictive parity): a precisão (precision), ou seja, a taxa de pessoas do que foram previstas como caso positivo e que realmente pertenciam à classe positiva deve ser igual nos sub grupos analisados. O que significa dizer:

\[\begin{equation} P(Y = 1 \mid d = 1, G = 0) = P(Y = 1 \mid d = 1, G = 1) \end{equation}\]

Calibração (Well calibration): Se o modelo diz que a probabilidade de ser da classe positiva é \(s\) para um conjunto de exemplos da base, então ao olhar para o resultado real, ela deve refletir a quantidade de pessoas na classe positiva quando dividida entre os sub grupos de interesse:

\[\begin{equation} P(Y = 1 \mid S = s, G = 0) = P(Y = 1 \mid S = s, G = 1) = s \end{equation}\]

Discriminação causal (causal discrimination): exemplos que possuam as mesmas características \(X\), exceto pela que determina os sub grupos de interesse, devem receber a mesma classificação:

\[\begin{equation} (X_{f} = X_{m} \land G_{f} \neq G_{m}) \rightarrow d_{f} = d_{m} \end{equation}\]

No final, a abertura no tema indica uma opotunidade enorme para pesquisa e debate, ainda mais pelo fato de algumas definições serem matematicamente imcompatíveis ³. Os resultados desse processo devem influenciar a maneira como essas questões serão tratadas nas futuras leis.

Extra: Podcast

Este texto foi feito a partir da pesquisa para participar do Podcast Hipsters.tech - Desafios em Machine Learning #137. Você pode ouvir o episódio aqui:

Bibliografia

		
		  @article{moneda2019bias-blogpost,
		  author = {Moneda, Luis},
		  title = Bias em Ciência de Dados,
		  journal = {Blogpost at lgmoneda.github.io},
		  year = {2019},
		  howpublished = {\url{lgmoneda.github.io}},
		  }